VOLUME 11 NUMBER 2 (July to December 2018)

by Jose B. Cruz, Jr.^1,* and Elvin Michael R. Almario²

¹National Academy of Science and Technology,
     Engineering Sciences and Technology Division, Bicutan, Taguig City, Philippines²Malayan Colleges Laguna, Pulo Diezmo Road, Cabuyao, Laguna 4025, Philippines

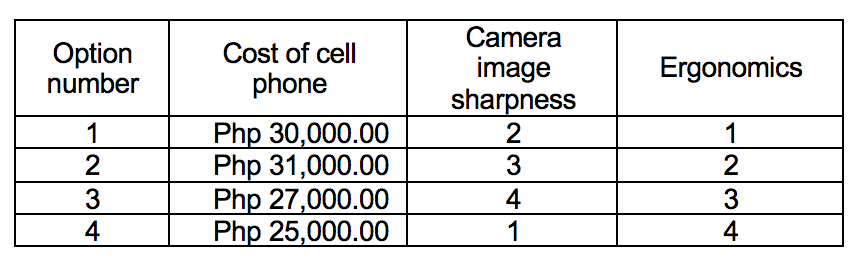
A simple procedure is described for selecting one option from a finite set or list of n options. Each option is associated with m performance criteria, features, or attributes. A weighted sum of the values of the normalized criteria is calculated for each option and the option with the largest weighted sum is selected. If the list contains Pareto-optimal options the winning option is Pareto optimal. It is shown that the winning option is invariant in spite of variations in the weights provided that these remain in a specified subspace of the multi-dimensional space of the weights that includes the chosen weights. Moreover, the winning option is invariant in spite of variations in the values of the multiple criteria provided that the variations remain in specified subspaces of the criteria space that includes the original criteria values. These invariance properties are reported for the first time in this paper. The entire process is called the invariance method. An upper bound for the maximum number of pairwise comparisons to identify all the k Pareto-optimal options in a finite set of n options, is derived. For each pair of n and k, where n is greater than or equal to k, there is a list such that the upper bound is reached.