VOLUME 14 NUMBER 2 (July to December 2021)

Azra May B. Kabiri*¹ and Guido David²

¹Institute of Mathematical Sciences and Physics,
      College of Arts and Sciences, University of the Philippines Los Baños,
      College 4031, Laguna, Philippines
²Institute of Mathematics, College of Science, University of the Philippines
      Diliman 1101, Quezon City, Philippines

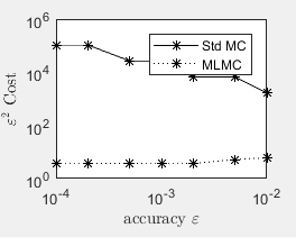
Asian options are path dependent options whose payoff depends on the average price of an asset. The price of these options does not have closed form solutions. The multilevel Monte Carlo is a method for discretization with the application of the standard Monte Carlo method. This method is easy to implement and has less computational cost than the standard Monte Carlo method. The application of this method in pricing Asian options whose underlying asset follows the geometric Brownian motion has already been studied. However, this has not been applied in pricing Asian options where the underlying asset follows the square root process. We use the Riemann scheme to discretize the temporal integral of the square root process and a simulation algorithm based on the transition density of the square root process to determine the values of the square root process at specified times. We determined that the rate of mean square convergence of the Riemann sum in approximating the temporal integral of the square root is at least of order 1. The results are compared with those obtained using standard Monte Carlo in terms of computational cost. It is shown that the use of this method with the Riemann scheme as discretization scheme is effective in terms of reducing computational cost as compared to the standard Monte Carlo method.