Solution to the <i>N</i> -Player Gambler’s Ruin with Variable Bet Sizes Using Recursions Based on Multigraphs

Marfil, Ramon Iñigo D.

VOLUME 16 NUMBER 1 (January to June 2023)

PSL%202021 vol14-no01-p12-28-Mikita%20and%20Padlan

SciEnggJ. 2023 16 (1) 040-047
available online: April 22, 2023

*Corresponding author
Email Address: rimarfil@math.upd.edu.ph
Date received: July 23, 2022
Date revised: February 18, 2023
Date accepted: February 24, 2023
DOI: https://doi.org/10.54645/2023161ESN-95

Read Full PDF

ARTICLE

Solution to the N -Player Gambler’s Ruin with Variable Bet Sizes Using Recursions Based on Multigraphs

Ramon Iñigo D. Marfil¹

¹Institute of Mathematics, University of the Philippines Diliman,
Quezon City, Philippines

KEYWORDS: Markov chain; graph theory; discrete mathematics; N-dimensional gambler’s ruin; applied probability

2020 MSC:60J10, 68R10, 91A06, 91A60

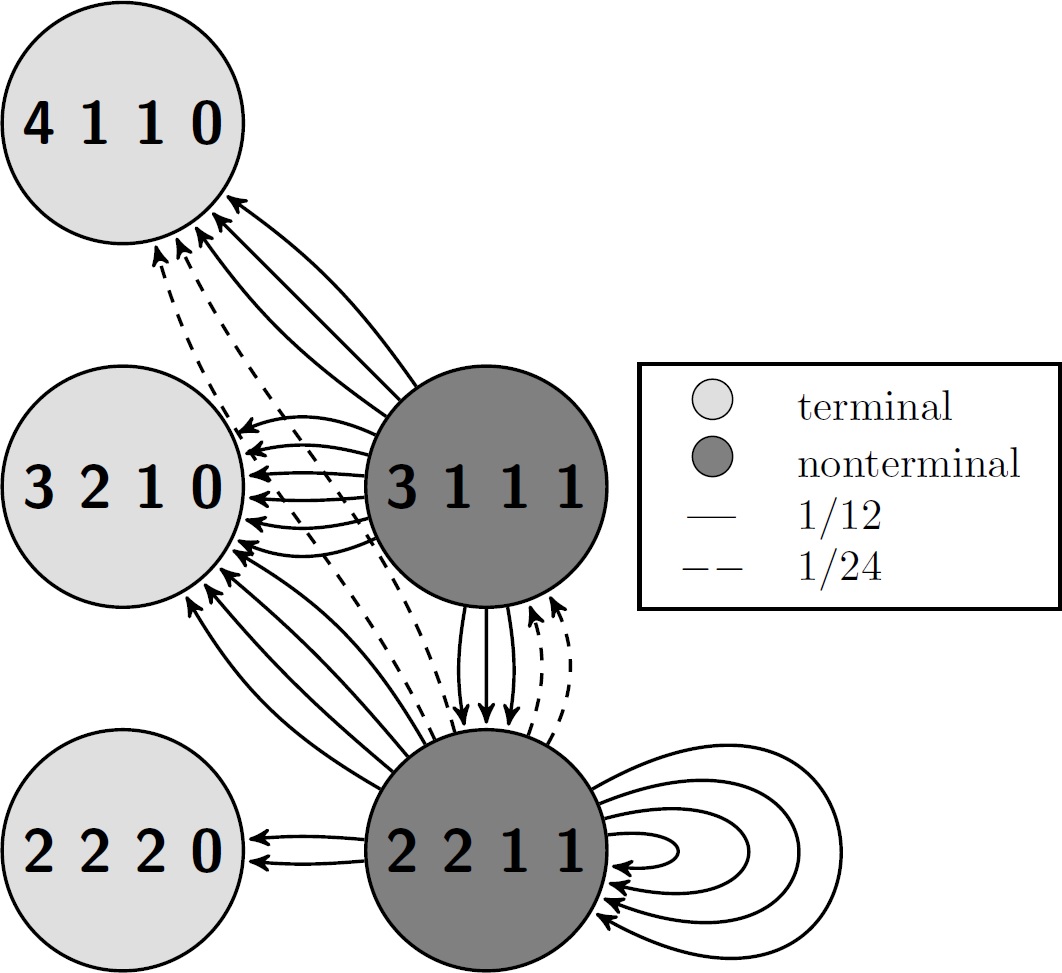
This paper studies the N -player gambler’s ruin with variable bet size, that is, more than one chip may be transferred from one player to another. Weighted directed multi- graphs were constructed to describe the transitions between chip states. Linear systems were constructed based on the connections between nodes in these graphs. Solutions for the placing probabilities of each player are obtained from these linear systems. Expected time until ruin is solved by modeling the game as a Markov process. A numerical algorithm was developed to solve the N -player gambler’s ruin with variable bet size for any positive integer chip total. Compared with the classic N -player gambler’s ruin, game durations are expected to be shorter due to the nature of bet sizes allowed in this model. Expected time until ruin and placing probabilities for All-In betting games are shown to be dependent only on the wealth proportion of the players.