Fragments that reduce the gap cap of the T-tetromino to six

Torres, Vince Jan F.; Vallejo, Louie John D.

VOLUME 17 NUMBER 1 (January to June 2024)

PSL%202021 vol14-no01-p12-28-Mikita%20and%20Padlan

SciEnggJ. 2024 17 (1) 128-133
available online: June 04, 2024
DOI: https://doi.org/10.54645/2024171OTN-38

*Corresponding author
Email Address: ldvallejo@math.upd.edu.ph
Date received: January 13, 2024
Date revised: March 30, 2024
Date accepted: April 25, 2024

Read Full PDF

ARTICLE

Fragments that reduce the gap cap of the T-tetromino to six

Vince Jan F. Torres and Louie John D. Vallejo*

Institute of Mathematics, College of Science, University of the
Philippines Diliman, Quezon City, Philippines

KEYWORDS: optimal tiling, monomino, tetromino, gap cap, tiling of rectangles

2020 MSC: 05B45, 52C20

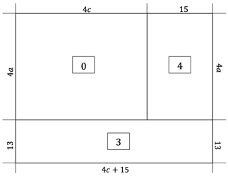
In 2015, it was established that at least nine monominoes are needed to tile all sufficiently large rectangles by T tetrominoes and monominoes. In this paper, we present tiling schemes that use special corner fragments to reduce this upper bound to six.