VOLUME 18 NUMBER 2 (July to December 2025)
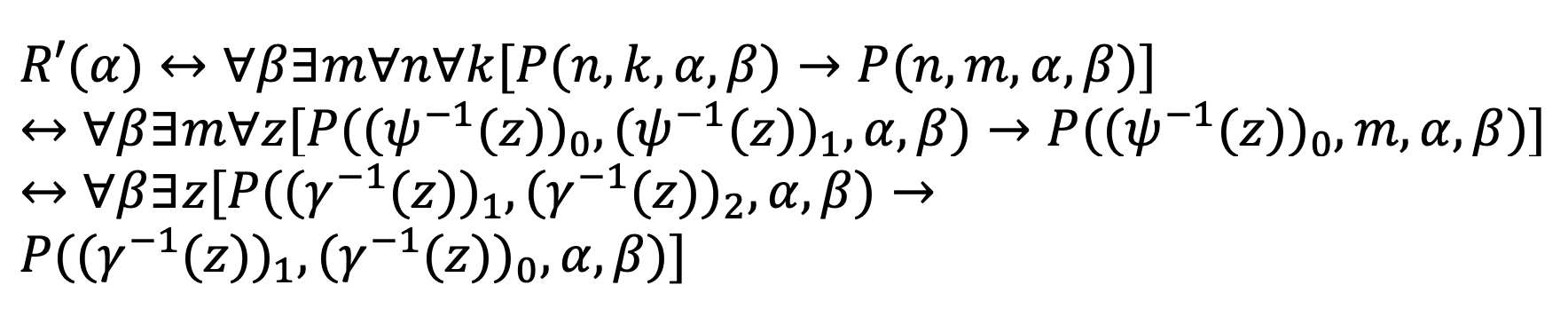
SciEnggJ. 2025 18 (2) 258-263
available online: 14 August 2025
DOI: https://doi.org/10.54645/2025182OAZ-78
*Corresponding author
Email Address: ablabao@up.edu.ph
Date received: 15 May 2025
Dates revised: 17 June 2025
Date accepted: 13 July 2025
ARTICLE
Effective descriptive complexity of some compact sets
University of the Philippines Diliman
Investigating the descriptive complexity of sets has been a topic of theoretical computer science, particularly general recursion theory. In this paper, we investigate the effective descriptive complexity of certain sets of real numbers, namely, compact sets corresponding to a countable collection of closed intervals under the standard euclidian topology. We derive the result that the descriptive complexity of defining such sets is Π_1^1, which corresponds to the descriptive complexity of well-orderings. To prove such a result, we define several functions and relations that could be effectively computed by some abstract computing machine with access to pre-loaded infinite inputs.
© 2025 SciEnggJ
Philippine-American Academy of Science and Engineering