VOLUME 19 NUMBER 1 (January to June 2026)

A mathematical framework for the detection of localized anomalies in the Young’s modulus of a rod

A critical issue that affects engineers trying to assess the structural integrity of various infrastructure, such as metal rods or acoustic ducts, is the challenge of detecting internal fractures (defects). Engineers typically rely on audible and visual inspection to detect these anomalies, as destructive testing is impractical. This study proposes a robust and non-invasive strategy to characterize such defects using only a small set of minimal measurements.

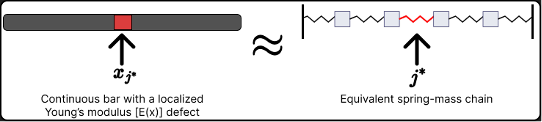
Assuming a one-dimensional model, we make use of the continuous one-dimensional wave equation to model these physical phenomena and then employ specialized mathematical analysis tools (the Laplace transform and optimization) to introduce our defect characterization ideas. In particular, we will focus on the case of a long rod which is homogeneous throughout except in a small area where a defect in its Young’s modulus is present. We will first demonstrate how the problem is equivalent to a spring-mass vibrational system. Afterwards, we show how our imaging strategy makes use of the Laplace domain analytic map between the characteristics of the respective defect and the measurement data.

More explicitly, we will utilize MATLAB to generate synthetic data as a computational surrogate for actual physical measurements in several scenarios with one defect of arbitrary location and stiffness. Subsequently, we will use this data along with our analytically developed map (between defect characteristics and measurements) to construct a residual function which, once optimized, will reveal the location and magnitude of the stiffness defect.